El diagrama de dispersión o gráfico de correlación es una herramienta empleada por su precisión en expresar la relación de dos variables de un conjunto de datos.
En este artículo se explica detalladamente su definición y los elementos que debes tomar en cuenta a la hora de construirlo. Así como ejemplos para establecer mejor el aprendizaje.
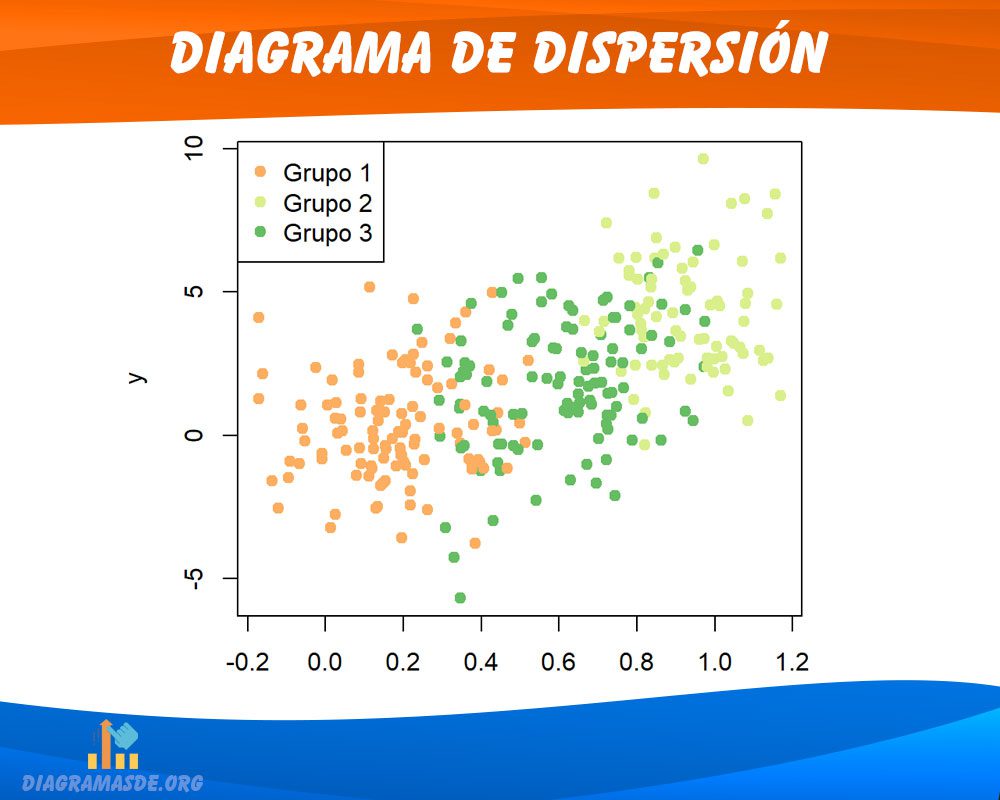
Tabla de Contenidos
¿Qué es un diagrama de dispersión?
El diagrama de dispersión es una expresión gráfica de la relación entre dos o tres variables cuantitativas sobre un mismo grupo de individuos o conjunto de datos. Este es un diagrama matemático basado en las coordenadas cartesianas (x,y) para mostrar dichos valores.
Los datos en este gráfico se representan a través de un conjunto de puntos, en el que cada uno expresa el valor de una variable que determina la posición en el plano cartesiano.En el que el eje horizontal (variable independiente x) y el valor de la otra variable, establecen la posición en el eje vertical (variable dependiente y), es decir que los puntos expresan la combinación de las dos variables.
Variable independiente x: Se representa en el eje de las abscisas y su valor no está determinado por la otra.
Por ejemplo: Por cada artículo que publiques obtienes $300
La variable independiente es la cantidad de artículos que publicas, ya que es la que puedes controlar.
Variable dependiente y: Se representa en el eje de las ordenadas y su valor lo determina la x.
En este caso es la cantidad de dinero que obtienes ya que está determinado por la cantidad de artículos que publiques.
Como dato curioso Galton, el padre del estudio de las bases genéticas de la capacidad cognitiva general, describió el proceso de elaboración de un diagrama de dispersión en un artículo de 1890.
Tipos de correlación en un gráfico de dispersión
Las variables tienen una relación recíproca lineal, es decir que son dependientes hasta cierto nivel, esto es lo que determina la correlación. Específicamente analiza la tendencia (creciente o decreciente) en los datos.
Fórmula del coeficiente de correlación de Pearson:

Donde: “x” representa a la variable número uno, “y” a la variable número dos, “zx” es la desviación estándar de la variable uno, “zy” es la desviación estándar de la variable dos y “N”, el número de datos.
La correlación ofrece una medición del signo y magnitud de la tendencia entre dos variables. Se describe a través del coeficiente de correlación. Una medida sin unidades que va desde -1 a +1 y se representa con la letra r . Existen tres clasificaciones:
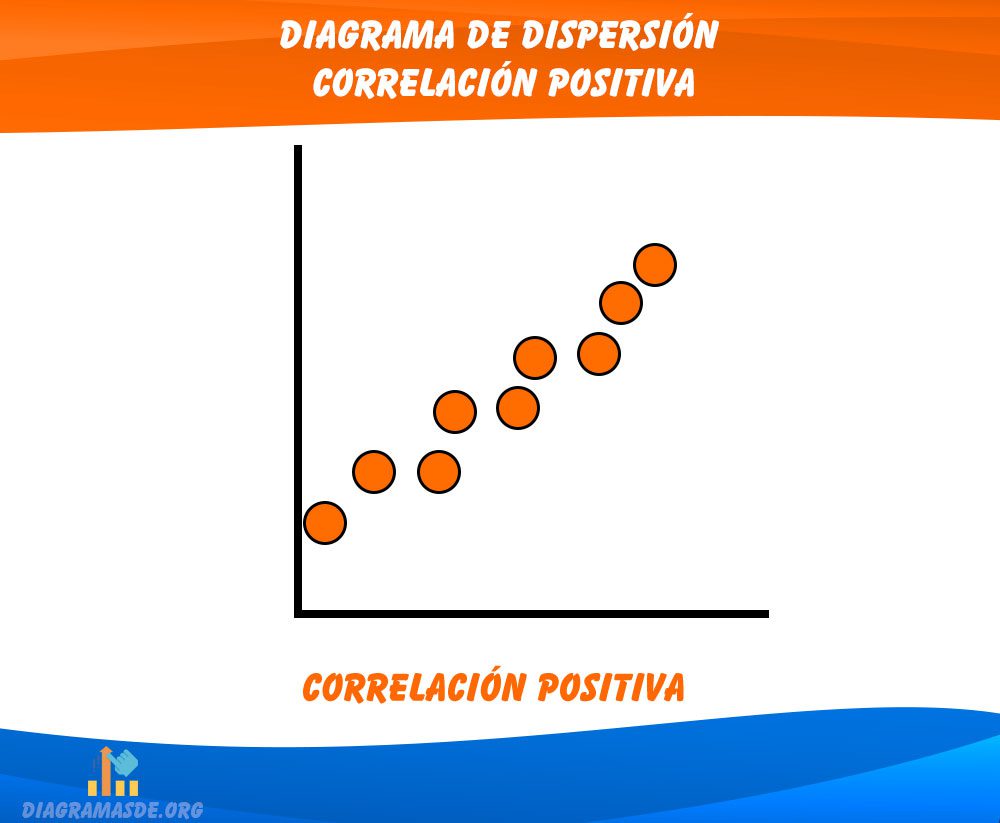
Correlación positiva : r > 0
Se muestra en las relaciones proporcionales cuando disminuyen o aumentan, es decir que se mueven en la misma dirección. Cuando r = 1 es una correlación positiva perfecta.
En la realidad no es común encontrar una correlación perfecta, a no ser que una medida sea efectivamente equivalente a la otra. Es común que este tipo nos indique que hay un error en los datos
El ejemplo más fácil para entenderla es el de la altura y el peso, ya que cuanto más alta es una persona, más pesada es.
Otro ejemplo de correlación positiva es la demanda y el precio. Ya que a medida que la primera suba, el segundo también y viceversa. El precio de un bien o servicio aumenta ya que más consumidores quieren adquirirlo y, por ende, van a pagar más por él.
Correlación negativa: r < 0
En este tipo la relación entre las variables es de sentido opuesto. Si una aumenta, la otra disminuye. Por lo general, a valores altos de una le corresponden los valores bajos de la otra y viceversa. Si r= -1 se debe correlación negativa perfecta
Un ejemplo sería la correlación negativa entre la oferta y el precio. Al disminuir la oferta sin que la demanda disminuya, los precios aumentan. La razón es que los mismos consumidores deben competir por un número reducido de productos, por lo que su valor incrementa.

Correlación nula: r = 0
Las variables no se relacionan, es decir que no hay dependencia. La nube de puntos se ve dispersa y redondeada.

En el siguiente grafico podemos ver todas las correlaciones del diagrama de dispersión.

Características del diagrama de dispersión
- Puede emplearse para analizar la relación entre variables de cualquier campo, psicología, demografía, economía, ingeniería, procesos industriales.
- Es una de las herramientas básicas de control de calidad
- Sirve para hacer predicciones a partir de la relación de las variables
- Se emplean para analizar la relación general de los datos como grupo
Pasos para elaborar un diagrama de dispersión
Ya sea para analizar la calidad de un producto, proceso industrial, tecnológico o mecánico, el procedimiento para hacer un gráfico de dispersión es el mismo.
Identificar la situación y las variables
El primer paso es que detectes el problema que deseas analizar. Lo siguiente es determinar las variables dependientes e independientes que definan la situación.
Por ejemplo, si se desea conocer la relación que hay entre la eficiencia terminal de la educación en México a nivel de bachillerato y el gasto público por alumno, hay que determinar las variables.

Ubicar los datos en el plano cartesiano.
Se expresan los datos en el eje de coordenadas para analizar la relación entre las variables. Los datos deben ubicarse dentro del mismo periodo de tiempo.
La variable x es el gasto público en educación. Es la dependiente
La variable y es la eficiencia terminal por alumno. Es la independiente.

Graficar las variables por par mediante círculos
Cuando dos pares de datos cumplen con el mismo valor, ambos deben ser dibujados uno al costado del otro o trazar el segundo punto a corta distancia.

Analizar los datos
En este punto debes analizar el diagrama para definir la correlación entre las variables, para el ejemplo interesa la eficiencia terminal y el gasto público. Hay que determinar la forma de la relación, la dirección y la fuerza que hay en la relación de las variables.
Cada uno de los puntos es la combinación de las variables, es decir que por cada año año en hay un nivel de gasto público y eficiencia. En el gráfico se muestra que el gasto público se ha incrementado con el paso de los años al igual que la eficiencia terminal.
Ejemplos de diagrama de dispersión o gráfico de correlación
Como ya lo hemos mencionado los gráficos de dispersión pueden aplicarse en diversos ámbitos. A continuación presentamos dos ejemplos que sirven para entender mejor su construcción.
Diagrama para determinar la calidad
El siguiente ejemplo se emplea para en el área de impresión de una empresa para determinar la relación entre la cantidad de tinta y el número de errores.


En el gráfico se visualiza que hay mucha cercanía entre los puntos, por lo tanto los valores se correlacionan estrechamente. Esto significa que la relación del aumento en los litros de tinta, influye en el número de errores en la impresión.
Diagrama en el deporte
En este otro ejemplo se representa el puesto ocupado por cada uno de los 20 equipos de primera división de la liga de fútbol en la
temporada 2005-2006 y los partidos empatados. (Un equipo de fútbol consigue tres puntos cuando gana un partido, 1 punto cuando empata y 0
puntos cuando pierde.)
La clasificación en la liga se realiza según el número total de puntos obtenido. El que más puntos consigue obtiene el
primer puesto –puesto 1–, el que menos puntos consigue obtiene el último puesto –puesto 20–).

El diagrama de dispersión es una herramienta muy útil cuando se desea entender la relación entre los valores de las variables de cualquier campo de estudio y nivel. Puede emplearse tanto a nivel de bachillerato como a nivel de doctorado.